Изготовление зубчатых колес. коэффициент смещения. точность зубчатых передач

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

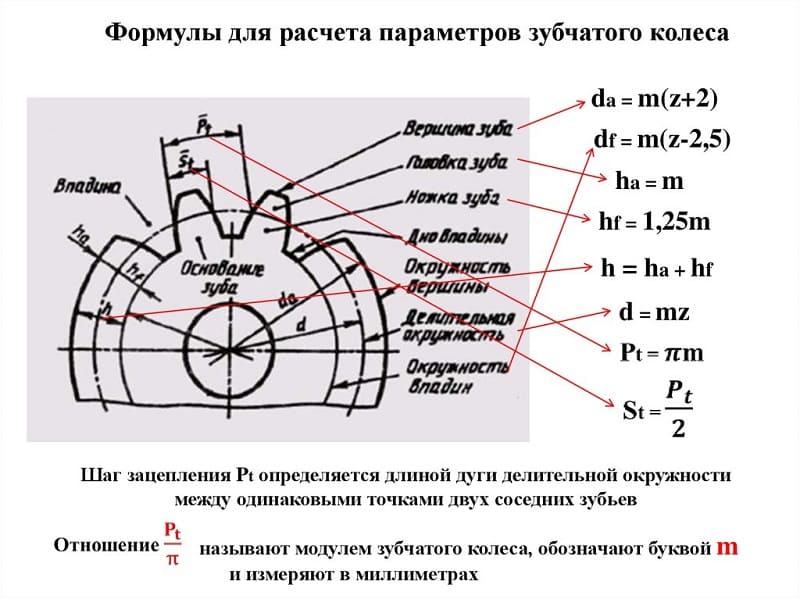
Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

Читать также: Измерение твердости металла по бринеллю

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

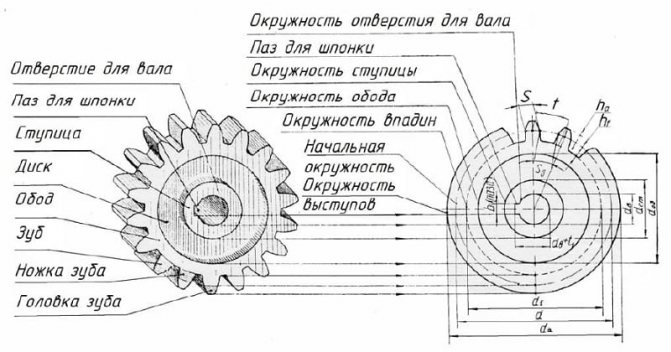
Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины

• для отлитых зубцов: sв=πm-1,53m=1,61m:
• для выполненных путем фрезерования- sв= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Как рассчитать передаточное число

Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.

Расчет без учета сопротивления

В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.

Где u12 – передаточное число шестерни и колеса;

Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.

Как обозначается точность изготовления зубчатых колес

При изготовлении любые их виды имеют ряд погрешностей, среди которых выделяют четыре основные:

• кинематическую погрешность, связанную в основном с радиальным биением зубчатых венцов;
• погрешность плавности работы, вызываемую отклонениями шага и профиля зубьев;
• погрешность контакта зубьев в передаче, которая характеризует полноту прилегания их поверхностей в зацеплении;
• боковой зазор между неработающими поверхностями зубьев.

Для контроля первых трех погрешностей стандартами установлены специальные показатели – степени точности от 1 до 12, причем точность изготовления увеличивается с уменьшением показателя. Для контроля четвертой погрешности изготовления имеются два показателя:

• вид сопряжения зубчатых колес – обозначается литерами A, B, C, D, E, H;
• допуск на боковой зазор – обозначается литерами x, y, z, a, b, c, d, e, h.

Для обоих показателей бокового зазора обозначения даны в порядке убывания его величины и допуска на него.

Условно точность зубчатых колес обозначается двумя способами. Если степень точности по первым трем погрешностям одинакова, то ставится один общий для них численный показатель степени точности, за которыми стоят литеры обозначения вида сопряжения и допуска на боковой зазор. Например:

8-Ас ГОСТ 1643 – 81.

Если точности по первым трем погрешностям разные, то в обозначении ставятся три численных показателя последовательно. Например:

5-4-3-Са ГОСТ 1643 – 81.

Эвольвентное зацепление

Эвольвентное зацепление — это зубчатая передача, которая нечувст­вительна к изменению межосевого расстоя­ния. Его изготавливают методом обкатки.

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут из­готавливаться на одном оборудовании, не­зависимо от количества зубьев и размеров головки.

Модули зацепления цилиндрических и ко­нических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных пе­редач по DIN 780; модули шлицевых соедине­ний по DIN 5480; модули зубчатого зацепле­ния нормального профиля для шестерен со спиральными зубьями по DIN 780.

Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; чер­вячных передач — DIN 3975; шлицевых соеди­нений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).

Форма зубьев гипоидных передач регла­ментируется стандартом DIN 867. В допол­нение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы заце­пления 12°, 14°30\ 15°, 17°30′_| 22°30′ и 25°.

Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)

Коррегирование зубчатого зацепления

Коррегирование зубчатого зацепления (из­менение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подреза­ния у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.

Зубчатые передачи с точно заданным межосевым расстоянием

У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса произво­дится на одинаковую величину, но в противо­положных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.

Зубчатые передачи с изменяемым межосевым расстоянием

Изменение высоты головки зуба для ше­стерни и зубчатого колеса производится независимо друг от друга, поэтому межосе­вое расстояние передачи может изменяться. Допускаемые отклонения линейных разме­ров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.

Подставляя j_η = 0 в приведенные ниже формулы, рассчитывают параметры за­цепления без зазора между зубьями. Для определения зазора между зубьями допу­скаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в за­висимости от требуемой степени точности зубчатой передачи. Следует отметить, что не обязательно стремиться к нулевому за­зору между зубьями. Для компенсации имею­щихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес. Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.

В таблице ниже приведены формулы для расчета зубчатой передачи:

Модуль — коническое колесо

К геометрии конических передач.

Модуль конического колеса меняется по длине зуба. За основной принимают окружной модуль на внешнем торце mte, который удобно измерять.
 

Рекомендуемые основные параметры конических передач.

Полученные значения модулей конических колес не округляют до стандартных, так как одним и тем же режущим инструментом можно нарезать колеса с различными модулями, лежащими в некотором непрерывном интервале значений. Принимать внешний окружной модуль меньше 1 5 мм нежелательно.
 

Высота зуба, шаг и модуль конического колеса переменны по длине зуба. Они максимальны на наружном дополнительном конусе и минимальны на внутреннем. По стандарту выбирают максимальный модуль т /, который определяет размеры зуба на развертке наружного дополнительного конуса.
 

Высота зуба, шаг и модуль конического колеса переменны по длине зуба. Они максимальны на наружном дополнительном конусе и минимальны на внутреннем. Для удобства измерения размеры конических колес принято определять по наружному торцу зуба, образованному наружным дополнительным конусом.
 

Метод предусматривает нарезание одной червячной фрезой определенного модуля конических колес с любым числом зубьев. Благодаря этому метод отличается универсальностью и находит применение в мелкосерийном производстве.
 

ГОСТа 9563 — 60; однако округление модуля конических колес не так существенно, как цилиндрических, так как здесь применение нестандартного модуля не вызывает необходимости в специальном зуборезном инструменте.
 

Номинальный модуль резца т0 и угол профиля ос0 могут не совпадать с параметрами тип нарезаемого колеса, так как получение необходимого угла профиля а на делительном конусе может быть обеспечено настройкой станка, а модуль конического колеса может быть нестандартным и дробным.
 

Значение модуля для конических и цилиндрических зубчатых колес одинаково. Модуль конических колес с пропорционально понижающейся высотой зуба определяется по внешнему диаметру в торцовом сечении, который принято называть окружным модулем tnt. При расчете конических колес с прямыми и криволинейными зубьями, в отличие от цилиндрических колес, полученный расчетным путем модуль можно не округлять до ближайшего стандартного значения.
 

Значение радиусов для профиля зуба при т мм.

Чертежи разрезов выполняются с соблюдением условностей изображения зубчатых колес в разрезах ( см. ГОСТ 3455 — 59, ГОСТ 3460 — 59, ГОСТ 9250 — 59), причем, если секущая плоскость проходит по зубу, то последний не штрихуется. Модуль конического колеса определяется измерением наибольшей высоты зуба ( фиг.
 

У конических колес одна и та же пара зубострогальных резцов формирует зуб по всей его длине, несмотря на то, что размеры зуба плавно уменьшаются по мере приближения к вершине конуса и в различных сечениях колеса модуль различен. Строгого соответствия номинального модуля резцов модулю нарезаемого колеса не требуется, допустимы отклонения в определенном диапазоне. Поэтому ряд модулей конических колес не регламентирован, внешний модуль может быть нестандартным и дробным.
 

Как и у цилиндрических колес, шаг и модуль плоского колеса переносятся в процессе нарезания по методу обкатывания с инструмента на начальный конус нарезаемого колеса. Для конических колес не делают различия между начальным и делительным конусами. Так как значение шага зависит от расстояния поперечного сечения колеса до вершины делительного конуса, то под шагом и модулем конического колеса подразумевают шаг pte и модуль те на делительной окружности его внешнего торца.
 

Основные параметры зубчатых цилиндрических передач

Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым

Межосевые расстояния

1 ряд	40	50	63	80	100	125	—	160	—	200	—	250	—	315	—	400
2 ряд	—	—	—	—	—	—	140	—	180	—	225	—	280	—	355	—
1 ряд	—	500	—	630	—	800	—	1000	—	1250	—	1600	—	2000	—	2500
2 ряд	450	—	560	—	710	—	900	—	1120	—	1400	—	1800	—	2240	—

1-й ряд следует предпочитать 2-му

Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения

Быстроходная ступень	40	50	63	80	100	125	140	160	180	200	225	250	280	315
Тихоходная ступень	63	80	100	125	160	200	225	250	280	315	355	400	450	500
Быстроходная ступень	355	400	450	500	560	630	710	800	900	1000	1120	1250	1400	1600
Тихоходная ступень	560	630	710	800	900	1000	1120	1250	1400	1600	1800	2000	2240	2500

Коэффициент запаса прочности при работе зуба двумя сторонами

Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах

Материал колес и термо- обработка	Отливки стальные и чугунные без термо- обработки	Отливки стальные и чугунные с термо- обработкой	Поковки стальные нормали- зованные или улучшенные	Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая)	Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой	Стальные с объемной закалкой	Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др.	Чугунные и пласт- массовые колеса
Коэфф.	1,9	1,7	1,5	2,2	1,4 — 1,6	1,8	1,2	1 — 1,2

Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения

Быстроходная ступень	40	50	63	80	100	125	140	160	180	200
Промежуточная ступень	63	80	100	125	160	200	225	250	280	315
Тихоходная ступень	100	125	160	200	250	315	355	400	450	500
Быстроходная ступень	225	250	280	315	355	400	450	500	560	630
Промежуточная ступень	355	400	450	500	560	630	710	800	900	1000
Тихоходная ступень	560	630	710	800	900	1000	1120	1250	1400	1600

Номинальные передаточные числа

1 ряд	1,0	—	1,25	—	1,6	—	2,0	—	2,5	—	3,15
2 ряд	—	1,12	—	1,4	—	1,8	—	2,24	—	2,8	—
1 ряд	—	4,0	—	5,0	—	6,3	—	8,0	—	10	—	12,5
2 ряд	3,55	—	4,5	—	5,6	—	7,1	—	9,0	—	11,2	—

1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5

Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25

Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.

При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.

ПРИЛОЖЕНИЕ 2 (рекомендуемое). ВЫБОР КОЭФФИЦИЕНТОВ СМЕЩЕНИЯ И КОЭФФИЦИЕНТОВ ИЗМЕНЕНИЯ РАСЧЕТНОЙ ТОЛЩИНЫ ЗУБА ИСХОДНОГО КОНТУРА

ПРИЛОЖЕНИЕ 2Рекомендуемое

1. В передачах с 1 шестерню рекомендуется выполнять с положительным смещением по табл.1, а колесо с равным ему по величине отрицательным смещением .

Таблица 1

Коэффициенты смещения для ортогональных конических зубчатых передач с прямыми зубьями при исходном контуре по ГОСТ 13754-81

Число зубьев шестерни	Значения коэффициента смещения при передаточном числе передачи
	1	1,12	1,25	1,4	1,6	1,8	2,0	2,5	3,15	4,0	5,0	6,3 и выше
12	—	—	—	—	—	—	—	0,50	0,53	0,56	0,57	0,58
13	—	—	—	—	—	—	0,44	0,48	0,52	0,54	0,55	0,56
14	—	—	—	0,27	0,34	0,38	0,42	0,47	0,50	0,52	0,53	0,54
15	—	—	0,18	0,25	0,31	0,36	0,40	0,45	0,48	0,50	0,51	0,52
16	—	0,10	0,17	0,24	0,30	0,35	0,38	0,43	0,46	0,48	0,49	0,50
18	0,00	0,09	0,15	0,22	0,28	0,33	0,36	0,40	0,43	0,45	0,46	0,47
20	0,00	0,08	0,14	0,20	0,26	0,30	0,34	0,37	0,40	0,42	0,43	0,44
25	0,00	0,07	0,13	0,18	0,23	0,26	0,29	0,33	0,36	0,38	0,39	0,40
30	0,00	0,06	0,11	0,15	0,19	0,22	0,25	0,28	0,31	0,33	0,34	0,35
40	0,00	0,05	0,09	0,12	0,15	0,18	0,20	0,22	0,24	0,26	0,27	0,28

Примечание. Данные таблицы могут быть использованы для неортогональных передач, если вместо и принимать соответственно и , а также для повышающих передач при 3,15, у исходного контура шестерни и соответственно уменьшенной у исходного контура колеса.Коэффициент изменения расчетной толщины зуба исходного контура положительный для шестерни и равный ему по величине, но обратный по знаку для колеса, рекомендуется вычислять по формуле

Формулой можно пользоваться для неортогональных передач, если заменить на , а также для повышающих передач при 3,15.Для ответственных тяжелонагруженных передач значения следует определять из расчета зубьев на изломную прочность.Для передач, у которых и отличается от указанных в табл.1, коэффициенты смещения принимаются с округлением в большую сторону.Для зубчатых колес, выполняемых не в соответствии со стандартным исходным контуром, коэффициенты смещения рекомендуется вычислять по формулам, приведенным в табл.2.

Таблица 2

Расчет коэффициентов смещения для ортогональных конических зубчатых колес с прямыми зубьями

Номер позиции	Расчетные зависимости
1
2
3
4
5
6
7	0,5 (2)·(4)·(6)
8
9	(8)-(7)
10	0,5 (6)
11	(3)·(10)
12	(10)++(9)
13	(11)+ -(9)
14
15
16
17
18
19
20
21
22	(12)·(20)
23	(13)·(21)
24	(22)
25	(23)
26	(22)-(23)
27	(7)-0,5 (26)
28	(26)·(27)
29	(7) (26)+(28)
30
31	(30)-(27)

Примечания:

1. Цифры в скобках соответствуют номерам позиций таблицы. определяется в результате последовательного выполнения действий по позициям 1-31. Исходные данные для расчета по табл.1 настоящего стандарта.

2. Расчетными формулами можно пользоваться и для неортогональных передач, если заменить и соответственно на и .

2. При 2,5 зубчатые колеса рекомендуется выполнять не только со смещением, устанавливаемым по п.1 настоящего приложения, но и с различной толщиной зуба исходного контура: увеличенной по сравнению с расчетной .

Настройка цепи дифференциала при обработке винтовых изделий.

Типичной является следующая формула:

где с — постоянная цепи;

β — угол наклона винтовой линии;

n — число заходов фрезы.

Продифференцировав обе части равенства, получим абсолютную погрешность di передаточного отношения

тогда допустимая относительная погрешность настройки

Если допустимое отклонение угла винтовой линии dβ выразить не в радианах, а в минутах, то получим

Например, если угол наклона винтовой линии изделия β = 18°, а допустимое отклонение в направлении зуба dβ = 4″ = 0′,067, то допустимая относительная погрешность настройки

δ = 0,067/3440*tg18 = 0,00006

Наоборот, зная относительную погрешность взятого передаточного отношения, можно по формуле (3) определить допущенную погрешность в угле винтовой линии в минутах. При установлении допустимой относительной погрешности можно в подобных случаях пользоваться тригонометрическими таблицами. Так, в формуле (2) передаточное отношение пропорционально sin β. По тригонометрическим таблицам для взятого числового примера видно, что sin 18° = 0,30902, а разность синусов на 1′ составляет 0,00028. Следовательно, относительная погрешность на 1′ составляет 0,00028 : 0,30902 = 0,0009. Допустимое отклонение винтовой линии — 0,067, поэтому допустимая погрешность передаточного отношения 0,0009*0,067 = 0,00006, такая же, как и при расчете по формуле (3). Когда оба сопряженных колеса нарезаются на одном станке и по одной настройке цепи дифференциала, то погрешности в направлении линий зубьев допускаются значительно большие, так как у обоих колес отклонения одинаковы и незначительно влияют только на боковой зазор при зацеплении сопряженных колес.

Расчет зубчатого колеса

Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.

Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.

1. Определение передаточного числа u.

2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.

3. Расчет зубьев передачи на изгиб.

4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).

5. Определение межосевого расстояния a_W из условия контактной прочности и округление его значения до стандартного.

6. Задание модуля из соотношения m = (0,01 — 0,02) х a_W и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.

7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.

8. Выбор коэффициентов формы зубьев для шестерни и колеса.

9. Проверка прочности зубьев по напряжениям изгиба.

10. Проведение геометрического расчета передачи.

11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.

Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.

Основные ошибки самостоятельной замены

Несмотря на предельно простую технологию, автолюбители часто допускают при замене венца следующие ошибки:

• перед тем, как снять зубчатый обод, следует произвести ревизию боковой плоскости маховика под сцепление, и отверстий для крепежных болтов;
• установка с перегревом отдельных участков венца приведет к быстрому износу зубьев именно на этих местах, так как происходит отпуск стали;
• наружный диаметр зубьев должен иметь фаску для плавного зацепления с бендиксом стартера без ударов.

Для того, чтобы уменьшить износ двигателя и увеличить приемистость машины на высоких оборотах, маховик часто облегчают. Из-за наличия дополнительных отверстий на наружном диаметре диска в зоне, примыкающей к зубчатому ободу, венец часто приваривается к диску.

Таким образом, венец можно заменить собственными силами при значительной выработке профиля зуба на отдельных участках. Снять обод можно на холодную, а при установке потребуется нагрев до 200 градусов максимум.

Анализ зубчатой передачи

Провести анализ качественных показателей зубчатой передачи — значит решить сложную оптимизационную задачу, содержащую большое количество параметров. Инженерам такие задачи приходится решать очень часто. Связано это с тем, что невозможно создать одинаково хорошее решение во всех аспектах — всегда приходится принимать определенные уступки.

Поэтому для проведения оптимизации каждый из параметров рассматривается по отдельности. Выделяется область его оптимальных значений, а затем все полученные области накладываются друг на друга с выделение такого решения, которое будет не самым лучшим, а удовлетворять наиболее важным требованиям надежности, экономичности и безопасности.

Качественные показатели зубчатой передачи — совокупность параметров, характеризующих зубчатых передачу с точки зрения надежности, контактной прочности, плавности передачи вращающего момента и долговечности. К таким параметрам относятся:

• коэффициент торцевого перекрытия
• коэффициенты удельного скольжения
• коэффициент удельного давления
• приведенные толщины зубьев по окружности вершин

Проведите расчет качественных показателей онлайн в калькуляторе, а затем приступайте к анализу! Задано межосевое расстояние? Тебе сюда!

Алгоритм анализа качественных показателей:

• Определить исходные данные из текста задания.
• Выбрать коэффициент смещения для колеса исходя из рекомендаций.
• Провести расчет геометрических параметров и качественных показателей, варьируя значения коэффициента смещения шестерни.
• Выделить область подрезания из условия:
• Выделить область заострения из условия:
• Выделить область технического заострения из условия:
• Определить область допустимых решений/значений (ОДР/ОДЗ)
• Оценить потенциально возможные значения коэффициента смещения шестерни по наличию стандартного инструмента, равномерному износу колес.

Результатом анализа является график качественных показателей и выбранный коэффициент смещения шестерни. Пример полученного графика:

График качественных показателей

Мы подготовили небольшое видео, в котором изложены основные этапы анализа качественных показателей:

Геометрический расчет элементов цилиндрической зубчатой передачи

Исходные данные для расчета:

• Модуль m = 4 мм;
• Число зубьев шестерни Z1 = 18;
• Число зубьев колеса Z2 = 30;
• Диаметр вала (ведущий) DB1 = 22 мм;
• Тип шпонки – Призматическая;
• Число шлицев Z – 8;
• Внутренний диаметр шлицев d = 22 мм;
• Диаметр вала (ведомый) DB2 = 30 мм;
• Ширина шлица b = 6 мм;
• Тип – D.

Результаты геометрического расчета цилиндрической зубчатой передачи

• Делительный диаметр шестерни d1=mz1=4×18=72 мм;
• Делительный диаметр колеса d2=mz2=4×30=120 мм;
• Высота головки зуба ha=m =4 мм;
• Высота ножки зуба hf=1,25m=1,25×4=5 мм;
• Высота зуба h=ha+hf=2,25m=2,25×4=9 мм;
• Диаметр вершин зубьев шестерни da1=d1+2ha1=72+2×4=80 мм;
• Диаметр впадин шестерни df1=d1-2hf=72-2×5=62 мм;
• Длина ступицы шестерни Lст1=1,5DB1=1,5×22=33 мм;
• Наружный диаметр ступицы шестерни Dст1=1,6DB1=1,6×22=35,2 мм;
• Диаметр вала шестерни D1=1,2×22=26,4 мм;
• Делительный диаметр колеса d2=mz2=4×30=120 мм;
• Диаметр вершин зубьев колеса da2=d2+2ha=120+2×4=128 мм;
• Диаметр впадин колеса df2=d2-2hf2=120-2×5=110 мм;
• Длина ступицы колеса Lст2=1,5DB2=1,5×30=45 мм;
• Наружный диаметр ступицы колеса Dст2=1,6DB2=1,6×30=48 мм;
• Диаметр вала колеса D2=1,2DB2=1,2×30=36 мм;
• Ширина зубчатого венца b=6m=6×4=24 мм;
• Толщина обода зубчатого венца δ1=2,25m=2,25×4=9 мм;
• Толщина диска δ2=1/3b=8 мм;
• Межосевое расстояние a=0,5(d1+d2)=0,5(72+120)=96 мм;
• Длина шлицев Lшл=(1,5. 2)Lст2=(1,5. 2)45=72 мм.

История

Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.

В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.

Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.

Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес .

Технологический процесс

Процесс изготовления шестерни на крупных производственных линиях максимально автоматизирован. Классический техпроцесс характеризуется следующими особенностями:

1. Для начала определяются основные параметры изделия, к примеру, число зубьев, модуль и степень точности геометрических размеров.
2. Следующий этап заключается в проведении заготовительной процедуры. Чаще всего проводится штамповка при использовании горизонтально-ковочной машины.
3. Для повышения эксплуатационных характеристик выполняется нормализация. Подобная термическая обработка позволяет снизить напряжения внутри материала.
4. Токарно-винторезная процедура позволяет получить заготовку требующихся размеров. Для этого выполняется точение поверхности и расточка фасок.
5. После механической обработки прямозубых шестерен выполняется повторно нормализация.
6. Заготовка подвергается зубофрезерной обработке. Для этого применяется полуавтомат 5306К или другое подобное оборудование.
7. Следующий шаг заключается в слесарной обработке. Технологический процесс определяет появление заусенец и других дефектов, которые устраняются при применении полуавтомата 5525. На линиях с низкой производительностью зачистка проводится ручным методом.
8. После получения зубьев выполняется термическая обработка, для чего часто применяется установка ТВЧ. Закалка позволяет существенно повысить твердость поверхности и ее износостойкость.
9. Шлифование поверхности. Для получения поверхности требуемого качества выполняется шлифовка. Есть довольно больше количество различного оборудования, которое подходит для шлифования самых различных поверхностей.
10. Большое распространение получили насадные шестерни. Они устанавливаются на валу, могут быть больших и малых размеров. Фиксация насадного варианта исполнения проводится за счет шпонки. Получить шпоночный паз можно при применении долбежного станка.
11. Зубошлифование также проводится при применении специальных станков.

https://youtube.com/watch?v=KbjmqvPM-1c

В заключение отметим, что процедура зубофрезервания достаточно сложна, предусматривает применение специального оборудования.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

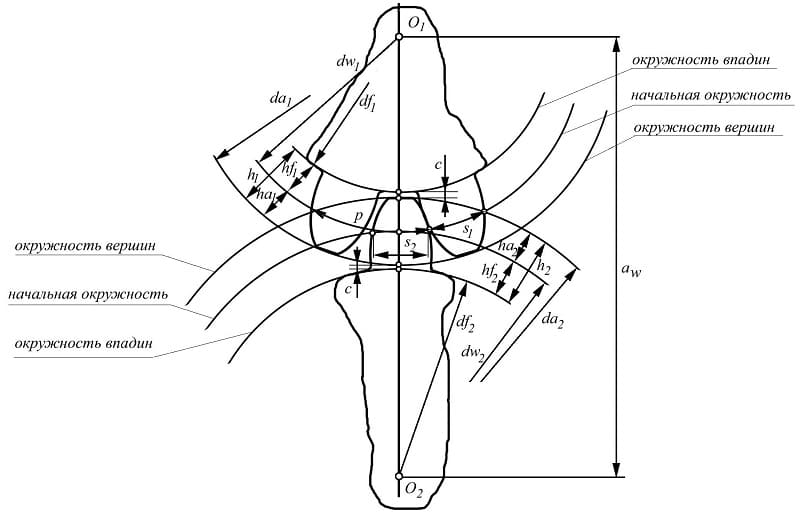
Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

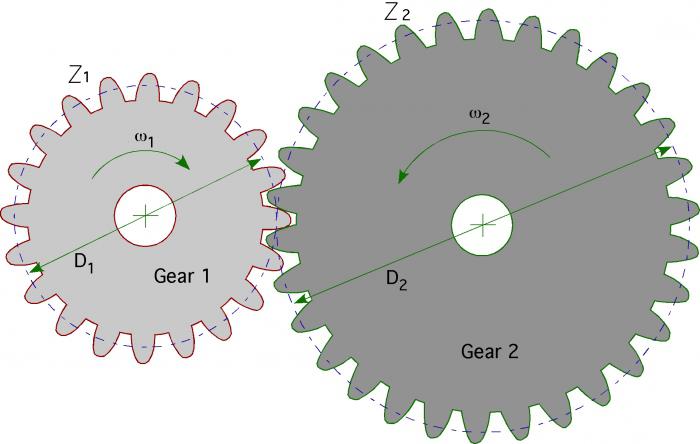
Уравнение зубчатой передачи

Она обменивает высокую входную скорость на больший выходной крутящий момент. Этот обмен происходит по очень простому уравнению, которое можно записать так:

Момент _{входной}* Скорость _{входная} = Момент _{выходной} * Скорость _{выходная}

Скорость входную можно найти, просто просматривая табличку приводного электродвигателя. Момент входной легко определить по этой скорости и механической мощности из той же таблички. Затем просто подставим выходную скорость или требуемый крутящий момент в правую часть уравнения.

Например, предположим, что ваш асинхронный двигатель при моменте на выходном валу 0,5 Н∙м имеет скорость 50 об/с, но вы хотите только 5 об/с. Тогда ваше уравнение будет выглядеть так:

0,5 Н∙м * 50 об/с = Момент _{выходной}* 5 об/с.

Ваш выходной крутящий момент будет 5 Н∙м.

Теперь предположим, что с тем же мотором вам нужно 5 Н∙м, но при этом требуется минимальная скорость 10 об/с. Как бы узнать, способен ли на это ваш мотор вместе с зубчатой передачей (т. е., по сути, мотор-редуктор)? Обратимся снова к нашему уравнению

0,5 Н∙м * 50 об/с = 5 Н∙м * Скорость _{выходная},

Скорость _{выходная} = 5 об/с.

Итак, вы определили, используя простое уравнение, что при показателе Момент _{выходной} =5 Н∙м обеспечить скорость выходную в 10 об/с ваша зубчатая передача не способна. Вы только что сохранили себе кучу денег, так как не потратили их на механизм, который никогда не заработал бы.

Настройка с учетом деформации винтов после обработки.

При нарезании метчиков с учетом усадки стали после последующей термической обработки или с учетом деформации винта вследствие нагревания при механической обработке, процент усадки или расширения непосредственно указывает на необходимое относительное отклонение в передаточном отношении сравнительно с тем, какое получилось бы без учета этих факторов. В этом случае относительное отклонение передаточного отношения в плюс или минус является уже не ошибкой, а преднамеренным отклонением.

Настройка делительных цепей. Типичная формула настройки

где р — постоянная;

z — число зубьев или других делений на один оборот заготовки.

Нормальный комплект из 35 колес обеспечивает абсолютно точную настройку до 100 делений, так как в числах зубьев колес содержатся все простые множители до 100. В такой настройке погрешность вообще недопустима, так как она равна:

где Δl — отклонение линии зуба на ширине заготовки В в мм;

пD — длина начальной окружности или соответствующей другой окружности изделия в мм;

s — подача вдоль оси заготовки на один ее оборот в мм.

Только в грубых случаях эта погрешность может не играть роли.

Конструкция и параметры зубчатого колеса

Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.

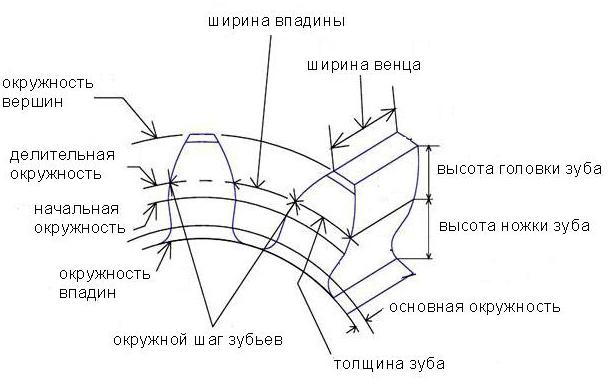
pmd

m = d/z= p/3,14, мм.

Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.

Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.

Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.