Изготовление зубчатых шестерен: процесс, технологии, станки

Ошибки при проектировании зубчатых колёс

Зуб, подрезанный у основания

Подрезание зуба

Согласно свойствам эвольвентного зацепления, прямолинейная часть исходного производящего контура зубчатой рейки и эвольвентная часть профиля зуба нарезаемого колеса касаются только на линии станочного зацепления. За пределами этой линии исходный производящий контур пересекает эвольвентный профиль зуба колеса, что приводит к подрезанию зуба у основания, а впадина между зубьями нарезаемого колеса получается более широкой. Подрезание уменьшает эвольвентную часть профиля зуба (что приводит к сокращению продолжительности зацепления каждой пары зубьев проектируемой передачи) и ослабляет зуб в его опасном сечении. Поэтому подрезание недопустимо. Чтобы подрезания не происходило, на конструкцию колеса накладываются геометрические ограничения, из которых определяется минимальное число зубьев, при котором они не будут подрезаны. Для стандартного инструмента это число равняется 17. Также подрезания можно избежать, применив способ изготовления зубчатых колёс, отличный от способа обкатки. Однако и в этом случае условия минимального числа зубьев нужно обязательно соблюдать, иначе впадины между зубьями меньшего колеса получатся столь тесными, что зубьям большего колеса изготовленной передачи будет недостаточно места для их движения и передача заклинится.

Заострение зуба

Для уменьшения габаритных размеров зубчатых передач колёса следует проектировать с малым числом зубьев. Поэтому при числе зубьев меньше 17, чтобы не происходило подрезания, колёса должны быть изготовлены со смещением инструмента — увеличением расстояния между инструментом и заготовкой (коррегированные зубчатые колеса).

Заострение зуба

Компьютерная модель зубчатой передачи (см. нанотехнологии)

При увеличении смещения инструмента толщина зуба будет уменьшаться. Это приводит к заострению зубьев. Опасность заострения особенно велика у колёс с малым числом зубьев (менее 17). Для предотвращения скалывания вершины заострённого зуба смещение инструмента ограничивают сверху.

Форма зуба

Зацепления различаются по профилю и типу зубьев. По форме зуба различают эвольвентные, круговые и циклоидальные зацепления. Наиболее часто используемыми являются эвольвентные зацепления. Они имеют технологическое превосходство. Нарезка зубьев может производиться простым реечным инструментом. Эти зацепления характеризуются постоянным передаточным отношением, не зависящим от смещения межцентрового расстояния. Но при больших мощностях проявляются недостатки, связанные с небольшим пятном контакта в двух выпуклых поверхностях зубьев. Это может приводить к поверхностным разрушениям и выкрашиванию материала поверхностей.

В круговых зацеплениях выпуклые зубья шестерни сцепляются с вогнутыми колесами и пятно контакта значительно увеличивается. Недостатком этих передач является то, что появляется трение в колёсных парах. Виды зубчатых колёс:

Прямозубые. Это наиболее часто используемый вид колёсных пар. Контактная линия у них параллельна оси вала. Прямозубые колёса сравнительно дешевы, но максимальный передаваемый момент у них меньше, чем у косозубых и шевронных колёс.
Косозубые. Рекомендуется применять при больших частотах вращения, они обеспечивают более плавный ход и уменьшение шума. Недостатком является повышенная нагрузка на подшипники из-за возникновения осевых усилий.
Шевронные. Обладают преимуществами косозубых колёсных пар и не нагружают подшипники осевыми силами, так как силы направлены в разные стороны.
Криволинейные. Применяются при больших передаточных отношениях. Менее шумные и лучше работают на изгиб.

Прямозубые колёсные пары имеют наибольшее распространение. Их легко проектировать, изготавливать и эксплуатировать.

Расчет параметров

Расчет параметров зубчатых колес выполняют комплексно, для всей передачи. Необходимость расчета отдельного колеса возникает только в процессе ремонта оборудования с неизвестными данными. Расчет начинают с определения требуемого числа зубьев и модуля зацепления. Для того чтобы узнать значение модуля, предварительно проводят расчеты на прочность, исходя из срока службы и выбранного материала будущего механизма. Также на этом этапе рассчитывают межосевое расстояние между колесами. На основе полученных данных выносливости зубьев вычисляется минимально допустимая величина модуля зацепления. Конкретное его значение выбирается на основе таблиц, приведенных в справочной литературе. Далее, используя требуемое передаточное отношение, производится вычисление числа зубьев на сопрягаемых колесах.

При известном модуле зацепления и количестве зубьев шестерни и колеса, доступно произвести вычисление геометрических размеров отдельных деталей. Основные диаметры и профиль зуба передачи рассчитываются с использованием несложных арифметических действий. Сложные операции потребуются только для ограниченного числа параметров. Для цилиндрического прямозубого колеса тригонометрические функции содержат только формулы расчета делительного диаметра. При проектировании других типов зубчатых колес, используют тот же математический аппарат, что и для прямозубых, но с добавлением расчетов, учитывающих иную геометрию деталей. Результаты расчетов используют для построения чертежей будущих шестерен, а также при вычислении параметров редукторов.

Заключительным этапом расчета зубчатой передачи становится окончательная проверка механизма на прочность. Если результаты этих вычислений укладываются в принятые нормативы, то полученные значения величин можно использовать для изготовления готового механизма. В противном случае может потребоваться выполнить новый расчет, изменив исходные данные, например, увеличить геометрические размеры, либо поменять тип зубчатой передачи или количество ступеней редуктора.

Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

Реечная передача (кремальера)

Реечная передача (кремальера) — один из видов механических передач, преобразующий вращательное движение ведущей шестерни в поступательное движение рейки. Используется в рулевом управлении большинства переднеприводных легковых автомобилей. Реечная передача (кремальера) применяется в тех случаях, когда необходимо преобразовать вращательное движение в поступательное и обратно. Состоит из обычной прямозубой шестерни и зубчатой планки (рейки). Работа такого механизма показана на рисунке.

Зубчатая рейка представляет собой часть колеса с бесконечным радиусом делительной окружности. Поэтому делительная окружность, а также окружности вершин и впадин превращаются в параллельные прямые линии. Эвольвентный профиль рейки также принимает прямолинейное очертание. Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс. Также реечная передача применяется в зубчатой железной дороге.

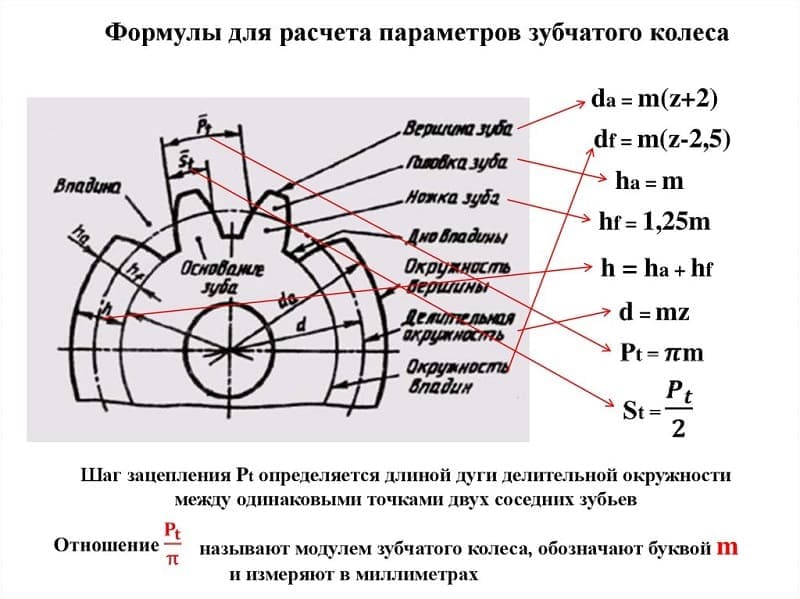
Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

Читать также: Измерение твердости металла по бринеллю

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

для отлитых зубцов: 1,53m:
для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины

для отлитых зубцов: sв=πm-1,53m=1,61m:
для выполненных путем фрезерования- sв= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

усилия, прикладываемые к детали при эксплуатации;
конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Расчет зубчатого колеса

Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.

Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.

1. Определение передаточного числа u.

2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.

3. Расчет зубьев передачи на изгиб.

4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).

5. Определение межосевого расстояния a_Wиз условия контактной прочности и округление его значения до стандартного.

6. Задание модуля из соотношения m = (0,01 — 0,02) х a_W и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.

7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.

8. Выбор коэффициентов формы зубьев для шестерни и колеса.

9. Проверка прочности зубьев по напряжениям изгиба.

10. Проведение геометрического расчета передачи.

11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.

Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.

Необходимые инструменты

Для проведения рассматриваемой процедуры требуется специальный режущий инструмент, которые позволяет проводить снятие требуемого количества материала. Довольно большое распространение получили следующие:

Если изготовление зубчатых колес проводится при применении технологии обкатки, то требуется эвольвентное зубчатое колесо, изготавливаемое при применении твердого и износостойкого материала.
Нарезка зубьев методом копирования проводится червячной фрезой. Она характеризуется определенной геометрией, которая позволяет получить впадины с заданными параметрами.

Также может устанавливаться пальцевая модульная фреза, которая устанавливается в специальном фрезеровальном оборудовании. Можно приобрести модульные фрезы для нарезания зубчатых колес, изготавливаемые при применении износостойких материалов.

Конструкция зубчатого колеса

Несмотря на кажущуюся простоту, в технике принято выделять несколько отдельных частей зубчатого колеса. Как и любое другое колесо, зубчатый вариант в своей основе имеет диск необходимого диаметра. Основной частью является обод, на боковой или торцевой поверхности которого выполнены зубья. Все вместе они образуют так называемый венец зубчатого колеса. Геометрия зубьев различна у разных типов зубчатой передачи. Сам зуб условно разбивается на несколько частей. Наружная часть называется вершиной. Прилегающие к ней боковые поверхности носят название головки зуба. Внутренняя часть именуется ножкой зуба. Две соседние ножки образуют впадину зубчатого колеса.

Для крепления на валу механизма в центре диска изготавливается ступица со сквозным отверстием. Форма отверстия зависит от геометрии сечения вала и может быть цилиндрической, квадратной или многоугольной. При использовании цилиндрических валов, в ступице обычно выполняют шпоночный паз.

С целью уменьшения веса толщина диска колеса выполняется обычно меньше, чем толщина ступицы или обода. Также для этого в теле диска могут присутствовать окна разнообразной формы.

Материалы для изготовления

Основной материал для изготовления колёсных пар — это сталь. Шестерня должна иметь более высокие прочностные характеристики, поэтому колёса часто изготавливают из разных материалов и подвергают разной термической или химико-термической обработке. Шестерни, изготовленные из легированной стали, подвергают поверхностному упрочнению методом азотирования, цементации или цианирования. Для углеродистых сталей используется поверхностная закалка.

Зубья должны обладать высокой поверхностной прочностью, а также более мягкой и вязкой сердцевиной. Это предохранит их от излома и износа поверхности. Колёсные пары тихоходных машин могут быть изготовлены из чугуна. В различных производствах применяются также бронза, латунь и различные пластики.

Зубчатая рейка

Геометрические параметры цилиндрических передач внешнего зацепления без смещения, мм

Шаг зубьев, мм	p = πm
Диаметр делительной окружности, мм	d = mz/cosβ
Диаметр окружности вершин, мм	d_a = d + 2m
Диаметр окружности впадин, мм	d_f = d – 2,5m
Межосевое расстояние, мм	a = m(z₁ + z₂)/(2cosβ)
Передаточное число	u = z₂/z₁
Коэффициент торцового перекрытия	ε_α = [1,88 – 3,2(1/z₁ + 1/z₂)]cosβ
Коэффициент осевого перекрытия	ε_β = bsinβ/(πm)
Примечание. Передаточное числоuпо ГОСТ 16532-70 определяется как отношение большего числа зубьев к меньшему независимо от того, как передается вращение: отz₁кz₂или отz₂кz₁.

Ширина зубчатых колес выбирается в
соответствии с установленными
эмпирическими соотношениями. В приводах
главного движения для уменьшения
концентрации нагрузки при высокой
твердости зубьев и высоких окружных
скоростях рекомендуется применять
относительно неширокие колеса и придавать
зубьям бочкообразную форму. Для прямозубых
колес ширина зубчатого венца b= (6…10)m, для косозубых
колес –b= (8…16)m.
Коэффициент ширины колес ψ_ba=b₂/aрекомендуется принимать равным 0,1 –
0,2. Численные значения ψ_baрегламентированы ГОСТом: 0,100; 0,125; 0,160;
0,200; 0,250 и т.д.

Учитывая возможное осевое смещение
зубчатых колес при сборке передачи,
ширину венца шестерни принимают на
несколько миллиметров большей, чем
ширину венца колеса:

b₁= 1,12b₂.

Межосевое расстояние aпо возможности рекомендуется округлять
по рядуRa40:…80; 85; 90;
95; 100; 105; 110; 120; 125; 130, далее через 10 до 260 и
через 20 до 420.

Минимальное число зубьев у меньшего
зубчатого колеса обычно ограничивается
условием неподрезания зубьев у основания,
для некорригированных передач z_min= 17. В станкостроении минимальное
число зубьев рекомендуется приниматьz_min= 21…24, а при работе передачи на высоких
оборотах для уменьшения шума целесообразно
братьz_min≥ 25. Общие рекомендации по выбору
числа зубьев шестерни некорригированной
передачи представлены в табл.2.32.

Таблица 2.32

Стандарты зубчатых передач США

Вместо модуля для стандартизации зубчатых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диаметра делительной окружности или диаметральный модуль (питч) (Р):

Пример HTML-страницы

Р = z/d = z/(z • m/25,4) =25,4/m

Для перевода стандарта США в европейский стандарт служит зависимость:

m = 25,4 мм / P

Размещение зубьев в пределах диаметрального модуля называется окружным шагом зацепления (CP):

CP = (25,4 мм / P) π.

Табл. Стандарты зубчатых передач

Полная высота зуба

В стандартах США полная высота зуба обозначается как высота головки h_a = т, что соответствует величине т в стандартах Германии.

Ножка зуба

Обозначается так же, как и полная высота зуба, но расчет головки зуба основывается на использовании своего модуля. Пример обозначения:

Обозначение (пример): Р 5 /7

Р = 7 для расчета головки зуба,

Р = 5 для расчета других параметров.

Система обозначений и преобразований

Диаметр окружности выступов: OD = d_a.

Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).

Диаметр окружности впадин: RD = d_f

Начальный диаметр:

LD =(N+2x) / P (в дюймах)

или

LD= (N+2x)·m (в мм).

LD ≈ d_w,

где d_w — диаметральный модуль.

Материалы для изготовления

Подытожим

Расчетные чертежи и схемы для шестеренок различных конфигураций преимущественно совпадают для косых и прямозубчатых версий. Основные различия возникают при расчетах на прочность. В графических отображениях применяются характеристики, ориентированные на типовые габаритные размеры шестеренок. Среди представленного ассортимента на рынке вполне реально подобрать зубчатое колесо с необходимыми характеристиками и прочностными показателями.

Не редко на конвейерных линиях из строя выходят узлы и агрегаты. Ремонт конвейерных лент от специалистов быстро вернет ваше оборудование в строй.

Передаточное число зубчатой передачи

Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.

Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.

Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.

Пример:

Момент _{входной} = 1,5 Н∙м, Скорость _{входная}= 100 об/с,

Передаточное число = 2/3

Момент _{выходной} = Момент _{входной} * 2/3 = 1 Н∙м,

Скорость _{выходная} = Скорость _{входная}* 3/2 = 150 об/с.

Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.

ОБЩИЕ ПОЛОЖЕНИЯ

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Принципиальная схема расчета геометрии приведена на чертеже.

1.2. Термины и обозначения, примененные в настоящем стандарте, соответствуют ГОСТ 16530-70* и ГОСТ 16531-70**. __________________ * Действует ГОСТ 16530-83; ** Действует ГОСТ 16531-83. – Примечание «КОДЕКС».

1.3. Наименования параметров, приводимых на рабочих чертежах зубчатых колес в соответствии с ГОСТ 2.403-75, а также межосевое расстояние зубчатой передачи, выделены в таблицах настоящего стандарта полужирным шрифтом.

1.4. При отсутствии в обозначениях параметров индексов «1» и «2», относящихся соответственно к шестерне и колесу, имеется в виду любое зубчатое колесо передачи.

1.5. При отсутствии дополнительных указаний везде, где упоминается профиль зуба, имеется в виду главный торцовый профиль зуба, являющийся эвольвентой основной окружности диаметра .

1.6. Расчетом определяются номинальные размеры зубчатой передачи и зубчатых колес.

1.7. Расчет некоторых геометрических и кинематических параметров, применяемых в расчете зубчатой передачи на прочность, приведен в приложении 5.

ГОСТ 9563—60 |СТ СЭВ 310—76)

Издание официальное

ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ

Москва

УДК 621.83/85 : 006.354

ГОСУДАРСТВЕННЫЙ СТАНДАРТ

Группа Г15 СОЮЗА ССР

Основные нормы взаимозаменяемости КОЛЕСА ЗУБЧАТЫЕ. МОДУЛИ

гост

9563-60* *

Basic norms of interchangeability. Gears. Modules

(СТ СЭВ 310—76)

Взамен ОСТ 1597

Утвержден Комитетом стандартов, мер и измерительных приборов при Совете Министров СССР 9 декабря 1960 г. Срок введения установлен

с 01.07,62

Проверен в 1979 г. Срок действия продлен до 01.01.89

Несоблюдение стандарта преследуется по закону

1. Настоящий стандарт распространяется на эвольвентные цилиндрические зубчатые колеса и конические зубчатые колеса с прямыми зубьями и устанавливает:

для цилиндрических колес —■ значения нормальных модулей; для конических колес — значения внешних окружных делительных модулей.

2. Числовые значения модулей должны соответствовать указанным в таблице.

1, 2. (Измененная редакция, Изм. № 1).

3—6. (Исключены, Изм. № 1).

мм

ЬЙ ряд	2-й ряд	1-й ряд	2-й ряд	1-й ряд	2-Й ряд	1-й ряд	2-й ряд
0,05		0,5		5		50
	0,055		0,55		5,5		55

Издание официальное Перепечатка воспрещена

* Переиздание (февраль 1987 г.) с Изменением № 1, утвержденным в июне 1979 г. (МУС 8—79).

мм

Продолжение

1-й ряд	2-й ряд	1-й ряд	2-й ряд	1-й ряд	2-Й ряд	1-й ряд	2-й ряд
0,06		0,6		6		60
	0,07		0,7		7		70
0,08		0,8		8		80
	0,09		0,9		9		90
0,1		1		10		100
	0,11		1,125		11
0,12		1,25		12
	0,14		1,375		14
0,15		1,5		16
	0,18		1,75		18
0,2		2		20
	0,22		2,25		22
0,25		2,5		25
	0,28		2,75		28
0,3		3		32
	0,35		3,5		36
0,4		4		40
	0,45		4,5		45

Примечания:

1. При выборе модулей ряд 1 следует предпочитать ряду 2.

2. Для цилиндрических зубчтатых колес допускается:

а) в тракторной промышленности применение модулей 3,75; 4,25; 6,5 мм;

б) в автомобильной промышленности применение модулей, отличающихся от установленных в настоящем стандарте.

3. Для конических зубчатых колес допускается:

а) определять модуль на среднем конусном расстоянии;

б) в технически обоснованных случаях применение модулей, отличающихся от указанных в таблице.

ПРИЛОЖЕНИЕ

Справочное

Информационные данные о соответствии ГОСТ 9563—60 и СТ СЭВ 310—66

Пункты ГОСТ 9563—60	Пункты СТ СЭВ 310—76
1	Вводная часть
2	Второй абзац

(Введено дополнительно, Изм. № 1).

Редактор Б. М. Лысенкина Технический редактор Э. В. Митяй Корректор С. И. Ковалева

Сдано в наб. 25.03.87 Подп. в печ. 14.07.87 0,25 уел. п. л. 0,25 уел. кр.-отт. 0,13 уч.-изд. л.

Тираж 8000 Цена 3 коп.

Ордена «Знак Почета» Издательство стандартов, 123840, Москва, ГСП,

Новопресненский пер., д. 3.

Вильнюсская типография Издательства стандартов, ул. Миндауго, 12/14. Зак. 1958.

Изменение № 2 ГОСТ 9563—60 Основные нормы взаимозаменяемости. Колеса зубчатые. Модули

Утверждено и введено в действие Постановлением Государственного комитета СССР по стандартам от 30.05.88 № 1547

Дата введения 01.01.89

Пункт 2 Таблица Примечание 2 дополнить перечислением — в: «в) в ре-дукторостроении применение модулей 1,6; 3,15; 6,3; 12,5».

Приложение исключить.

(ИУС № 9 1988 г.)

Цилиндрические зубчатые колёса [ править | править код ]

Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.

Параметры эвольвентного зубчатого колеса:

m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:

>> >

z — число зубьев колеса
p — шаг зубьев (отмечен сиреневым цветом)
d — диаметр делительной окружности (отмечена жёлтым цветом)
d_a — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
d_b — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
d_f — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
h_aP+h_fP — высота зуба тёмного колеса, x+h_aP+h_fP — высота зуба светлого колеса

В машиностроении приняты определённые значение модуля зубчатого колеса m для удобства изготовления и замены зубчатых колёс, представляющие собой целые числа или числа с десятичной дробью: 0,5; 0,7; 1; 1,25; 1,5; 1,75; 2; 2,5; 3; 3,5; 4; 4,5; 5 и так далее до 50. (подробнее см. ГОСТ 9563-60 Колеса зубчатые. Модули)

Высота головки зуба — h_aP и высота ножки зуба — h_fP — в случае т. н. нулевого зубчатого колеса (изготовленного без смещения, зубчатое колесо с «нулевыми» зубцами) (смещение режущей рейки, нарезающей зубцы, ближе или дальше к заготовке, причем смещение ближе к заготовке наз. отрицательным смещением, а смещение дальше от заготовки наз. положительным) соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,25 m, то есть:

h f P h a P = 1 , 25 >>>=1,25> >

Отсюда получаем, что высота зуба h (на рисунке не обозначена):

h = h f P + h a P = 2 , 25 m >+>=2,25m> >

Вообще из рисунка ясно, что диаметр окружности вершин d_a больше диаметра окружности впадин d_f на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр d_a и результат разделить на число зубьев z плюс 2:

m = d a z + 2 >> >

Продольная линия зуба

Зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:

17. Длина общей нормали цилиндрических прямозубых колес

Измерение толщины зубьев при длине общей нормали W имеет то преимущество перед измерением по постоянной хорде, что не требуется более точного изготовления зубчатых колес по наружному диаметру.

Для прямозубых колес без смещения

для колес со смешением (при коэффициенте смещения х)

здесь W’ — длина общей нормали цилиндрических прямозубых колес при m_n = 1. Значения W’ в зависимости от числа зубьев колеса и числа зубьев, охватываемых при измерении, указаны в таблице, приведенной ниже.

Дайна общей нормали W’ цилиндрических прямозубых колес при m_n = 1 мм

Зубчатые передачи

Достоинства: практически неограниченная передаваемая мощность малые габариты и вес стабильное передаточное отношение высокий КПД, который составляет в среднем 0,97 — 0,98

Недостатки: шум в работе на высоких скоростях (может быть снижен при применении зубьев соответствующей геометрической формы и улучшении качества обработки профилей зубьев)

Преимущественное распространение получили передачи с зубьями эвольвентного профиля, которые изготавливаются массовым методом обкатки на зубофрезерных или зубодолбежных станках. Достоинство эвольвентного зацепления состоит в том, что оно мало чувствительно к колебанию межцентрового расстояния

При высоких угловых скоростях вращения рекомендуется применять косозубые шестерни, в которых зубья входят о зацепление плавно, что и обеспечивает относительно бесшумную работу. Недостатком косозубых шестерен является наличие осевых усилий, которые дополнительно нагружают подшипники. Этот недостаток можно устранить, применив сдвоенные шестерни с равнонаправленными спиралями зубьев или шевронные шестерни. Шевронные шестерни, ввиду высокой стоимости и трудности изготовления применяются сравнительно редко — лишь для уникальных передач большой мощности. При малых угловых скоростях вращения применяются конические прямозубые шестерни, при больших — шестерни с круговым зубом, которые в настоящее время заменили конические косозубые шестерни, применяемые ранее. Конические гипоидные шестерни тоже имеют круговой зуб, однако оси колес в них смещены, что создает особенно плавную и бесшумную работу. Передаточное отнесение в зубчатых парах колеблется в широких пределах, однако обычно оно равно 3 — 5

История

Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.

В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.

Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.

Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес .

Основные определения из теории зацепления шестерен

Начальными называются воображаемые окружности, которые при зацеплении шестерен катятся без скольжения одна по другой

Делительными называются воображаемые окружности, по которым происходит номинальное деление зубьев. Для них справедливо уравнение: d _д = mZ Если шестерни не имеют коррекции, то начальные и делительные окружности совпадают

Окружностями выступов и впадин называются окружности, ограничивающие вершины и впадины зубьев

Основными называются окружности, по которым развертываются эвольвенты, очерчивающие профили зубьев d = d _дcosα

Шагом t называется расстояние по дуге делительной окружности между одноименными профилями соседних зубьев

Основным шагом t называется шаг по основной окружности

Модулем называется отношение диаметра делительной окружности к числу зубьев или шага к π

Ритчем р называется число зубьев, приходящееся на один дюйм делительной окружности

Линией зацепления ЛЗ называется геометрическое место точек контакта зубьев в зацеплении. В эвольвентном зацеплении ЛЗ — прямая, нормальная к профилю зубьев в полюсе зацепления и касательная к основным окружностям

Углом зацепления α называется угол между линией зацепления и перпендикуляром к линии центров

Углом наклона спирали зубьев косозубых шестерен β называется угол между осью зуба и образующей делительного цилиндра или конуса

Коэффициентом перекрытия ε называется отношение дуги зацепления к основному шагу

Коэффициентом коррекции ξ называется отношение величины профильного смещения к модулю

Основные геометрические параметры

Построение кинематической схемы, технические характеристики, способы обработки отдельных деталей этих механизмов задаются геометрической формой отдельных элементов. Основными геометрическими параметрами, которые рассчитываются при проектировании являются:

углы делительных конусов (каждого колеса или шестерёнки);
диаметры всех элементов (обоих валов, ведущих и ведомых шестерён);
внешний окружной модуль шестерни;
расстояние от вершины конуса до его образующей (называется делительное расстояние);
расстояние между осей;
радиальный зазор применяемых подшипников;
делительный диаметр (он определяет величину зуба шестерёнки);
диаметр углублений и верхней части зубьев.

Для удобства проведения расчетов и понимания механизма зацепления вводят три вида торцовых сечений. Это сечения во внешней, внутренней и средней части каждого зуба.

Уменьшение толщины зубьев по направлению к вершине приводит к созданию надежного зацепления во время движения. Угол наклона по направлению к вершине определяет параметры, задаваемые при обработке.

Под линией зубьев понимают пересечение двух прямых. Одна образована боковой поверхностью зуба, вторая является краем делительной конической поверхности.

Для улучшения эксплуатационных характеристик — повышения износостойкости, сопротивления при контакте, уменьшение заедания и лучшей передачи коническим зубчатым колёсам энергии вращения используют метод выравнивания коэффициентов удельного скольжения.

С этой целью колесо и шестерню стараются изготовить с одинаковыми параметрами смещения, но с разными знаками. Например, для шестерни задают параметр со знаком плюс, а для колеса со знаком минус.

Основные геометрические соотношения задаются на этапе разработки всего механизма конической передачи качество передачи. Геометрические параметры рассчитываются на основании известных соотношений.