Построение правильного шестигранника

Построение на плоскости

Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи: http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?ins >

Нам понадобятся: карандаш, линейка, циркуль.

Построение угла в 60

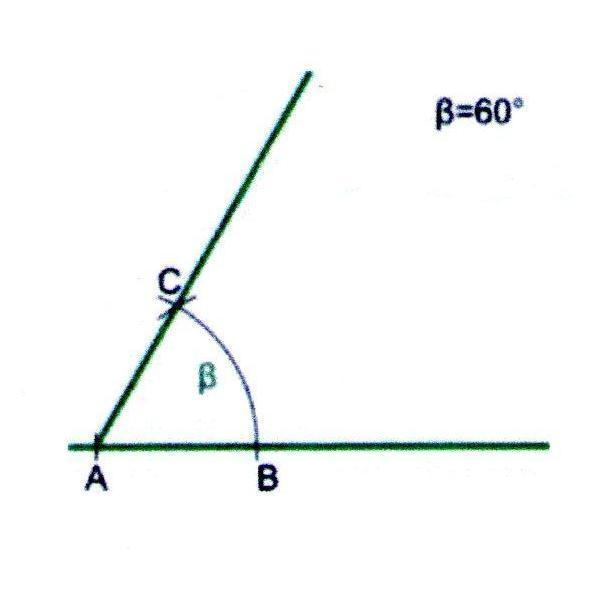
1. Проведём прямую и отметим на ней точку А.

2. Из точки А проведём дугу произвольного радиуса и получим точку В.

3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.

4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.

Построение угла в 45

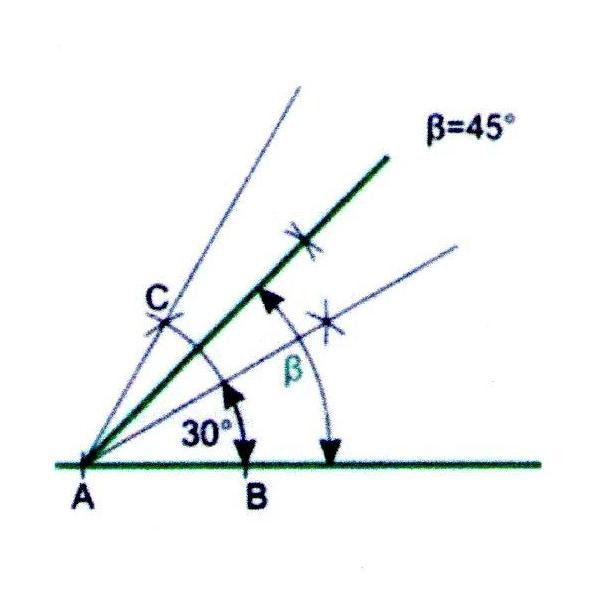
1. Построим угол 60, кака описано выше.

2. Разделим полученный угол пополам.

3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.

Построение угла в 75

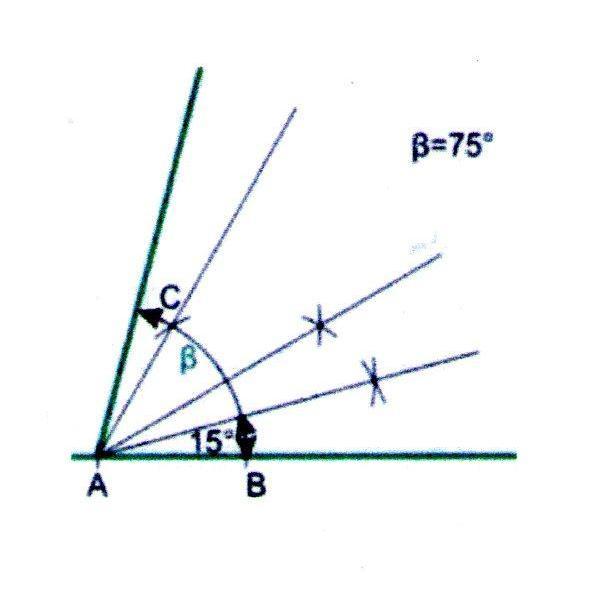
2. В ходе дальнейшего деления надвое получим угол в 15.

3. Отразим угол в 15 через луч 60 и так получим угол в 75.

Построение угла в 90

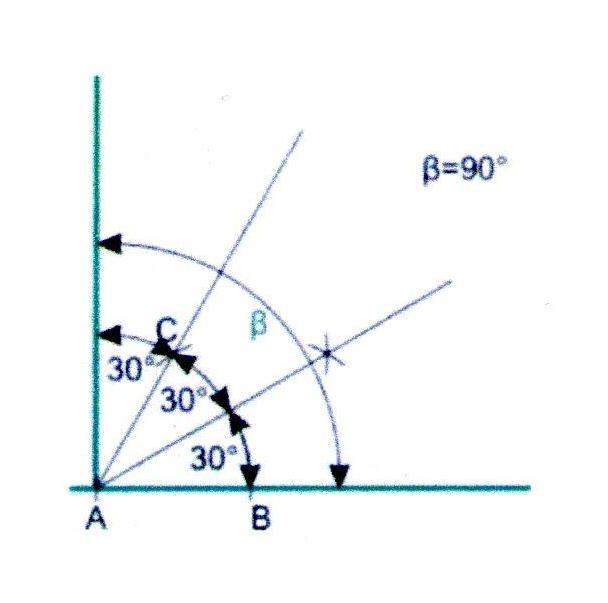
1. Построим угол в 60, как описано выше, и разделим его пополам.

2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.

Разделение отрезка на равные части.

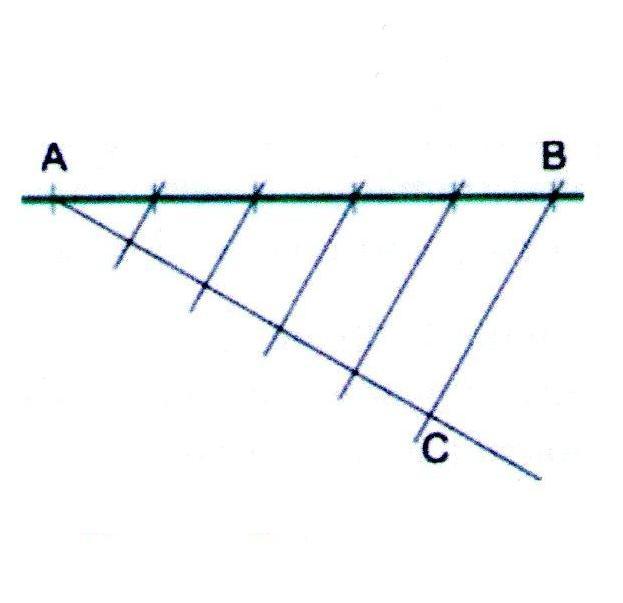
1. Проведём прямую и отметим на ней отрезок АВ.

2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.

3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.

Построение правильного пятиугольника.

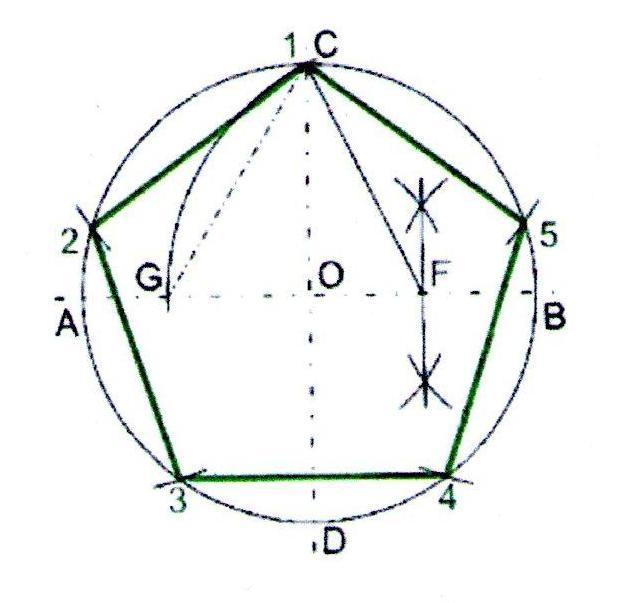
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC . Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G .

3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG .

Построение правильного шестиугольника.

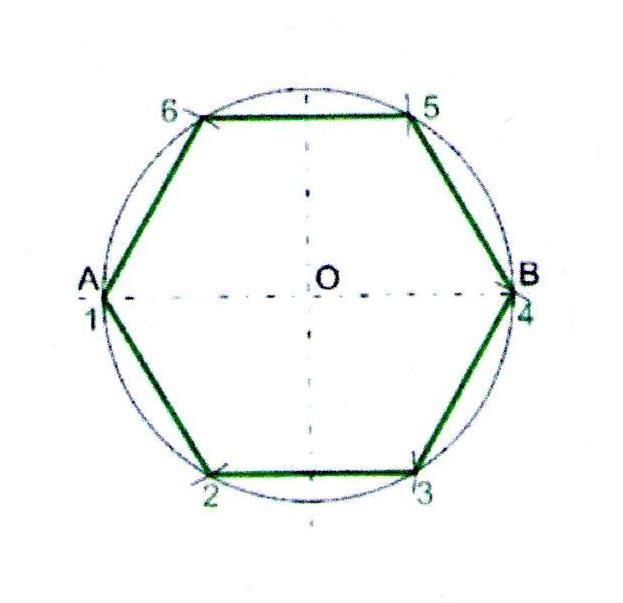
1. Проведём окружность радиусом 50 мм.

2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.

Построение правильного семиугольника.

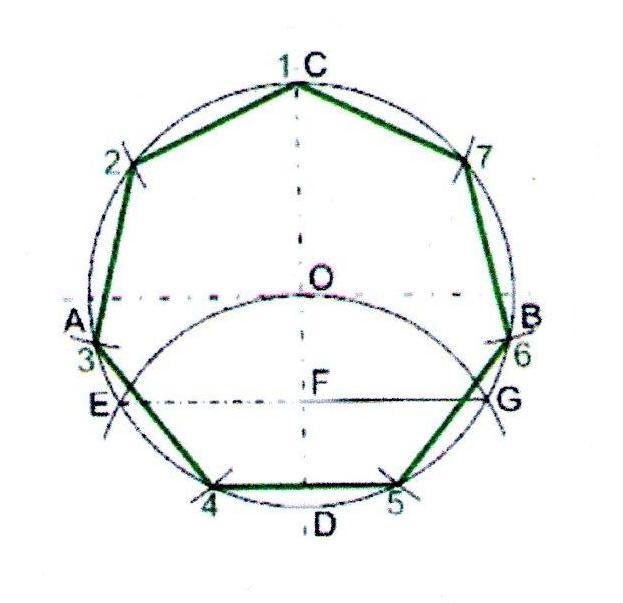
1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Из точки D проведём дугу радиусом равным радиусу окружности.

3. Дуга пересечёт окружность в точках E и G .

4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF .

Общий метод построения многоугольников.

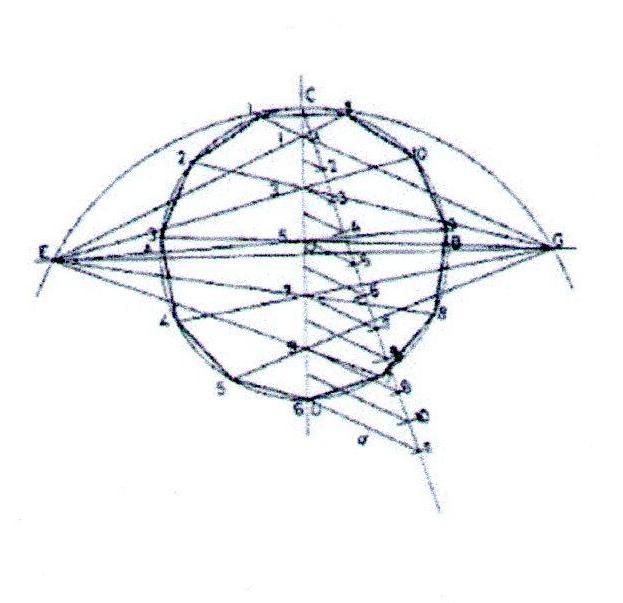
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.

2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.

3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.

4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G . Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Читать также: Каким проводом делать заземление

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

1. диаметр описанной окружности;
2. диаметр вписанной окружности;
3. площадь;
4. периметр.

Описанная окружность и возможность построения

Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

R=а.

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

S=πR²

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

1. Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
2. Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
3. Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

Читать также: Схема последовательного подключения лампочек с выключателем

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

1. Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
2. Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
3. Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
4. Углы новообразованного шестиугольника равняются 360-120-60-60=120°.

Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:

d=а(√3)/3

Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:

r₂=а/2

Площадь нового шестиугольника можно посчитать так:

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

1. Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
2. Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
3. Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
4. После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
5. Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
6. Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
7. На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

1. Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
2. Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
3. Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
4. Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
5. Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
6. D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Как правильно изобразить шестигранную призму?

Шестигранная призма строится уже значительно сложнее. Можно идти по принципу построения четырехгранной призмы, где сначала обозначается основа, а затем достраиваются боковые грани. Можно строить иначе. Для того, чтобы правильно построить шестигранную призму, мы должны построить четырехгранную.

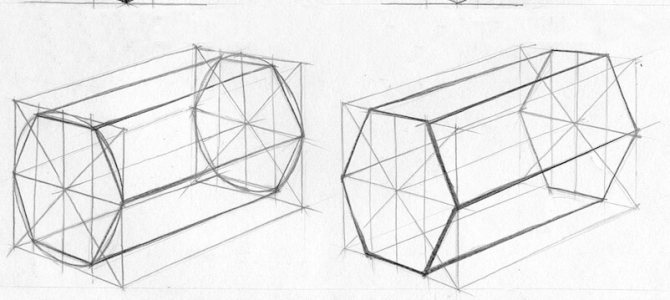
При этом мы делим переднюю грань пополам, создавая дополнительные грани. Этот способ сложнее, так как ошибка на первом этапе может испортить итоговый результат. Шестигранную призму мы строим с применениями знаний о раскрытии эллипсов, что способствует правильному определению размеров граней. Как и любой предмет, объемность призмы создается с помощью светотени. Начинаем штриховку равномерно, после чего добираем тон в самых темных участках.

Построение правильного четырехугольника вписанного в окружность

Вариант 1

Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3. 

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

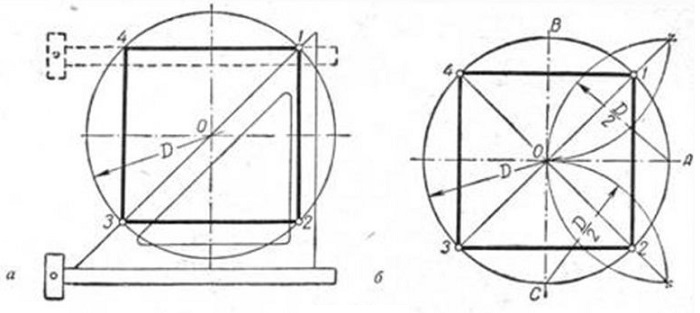
Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения. 

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

Шестиугольник, виды, свойства и формулы

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник, выпуклый и невыпуклый шестиугольник

Правильный шестиугольник (понятие и определение)

Свойства правильного шестиугольника

Формулы правильного шестиугольника

Правильный шестиугольник в природе, технике и культуре

Звездчатый шестиугольник

Восьмиугольник

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник – это многоугольник с шестью углами.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый шестиугольник

  Рис. 2. Невыпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

Правильный шестиугольник (понятие и определение):

Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Рис. 3. Правильный шестиугольник

Правильный шестиугольник имеет 6  сторон, 6 углов и 6 вершин.

Углы правильного шестиугольника образуют шесть равносторонних треугольников.

Правильный шестиугольник можно построить с помощью циркуля и линейки.

Свойства правильного шестиугольника:

1. Все стороны правильного шестиугольника равны между собой.

a1 = a2 = a3 = a4= a5 = a6. 

2. Все углы равны между собой и составляют 120°.

α1 = α2 = α3 = α4 = α5 = α6 = 120°.

Рис. 4. Правильный шестиугольник

3. Сумма внутренних углов любого правильного шестиугольника равна 720°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.

Рис. 5. Правильный шестиугольник

5. Количество диагоналей правильного шестиугольника равно 9.

Рис. 6. Правильный шестиугольник

6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.

Рис. 7. Правильный шестиугольник

7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).

8. Радиус описанной окружности правильного шестиугольника и его сторона равны.

Рис. 8. Правильный шестиугольник

R = a

Правильный шестиугольник в природе, технике и культуре:

Пчелиные соты имеют форму правильного шестиугольника.

Графит, графен имеют гексагональную кристаллическую решетку.

Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.

Рис. 9. Гигантский гексагон на Сатурне

Сечение гайки и многих карандашей имеет вид правильного шестиугольника.

Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.

Панцирь черепахи состоит из шестиугольников.

Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.

Рис. 10. Материковая часть Франции

Формулы правильного шестиугольника:

Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.

Формулы периметра правильного шестиугольника:

Формулы площади правильного шестиугольника:

Формула радиуса окружности, вписанной в правильный шестиугольник:

Формула радиуса окружности, описанной вокруг правильного шестиугольника:

R = a

Звездчатый шестиугольник:

Звездчатый шестиугольник (гексаграмма) – это многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника.

Гексаграмма (др.-греч. ἕξ – «шесть» и γραμμή – «черта, линия») – это звезда с шестью углами, которая образуется из двух наложенных друг на друга равносторонних треугольников.

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

Примечание:  Фото https://www.pexels.com, https://pixabay.com

Еще технологии…

карта сайта

Способ вычерчивания шестиугольника без циркуля

Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины – специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.

Способ построения выглядит следующим образом:

Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 – углы, 0 – центр, D – радиус шестигранника.

• к одной стороне отрезка прикладывается угольник – короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
• на листе/заготовке вычерчивается линия – длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
• операция повторяется при развороте угольника – угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
• разворот угольника – теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
• уточнение размеров сторон – на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
• строительство двух оставшихся сторон – они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
• контроль параллельности – шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком

Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.

Третий способ вычерчивания шестиугольника циркулем: a – диаметр, b – сторона шестигранника.

В последнем случае удобнее несколько изменить технологию:

• после вычерчивания центрального отрезка по нему выравнивается рейсшина;
• инструмент откатывается вниз на произвольную величину;
• короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
• скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.

Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.

Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.

Здравствуйте коллеги. В этом уроке узнаем, как нарисовать шестиугольник в перспективе.

Как вписать его фронтально в окружность мы смотрели в прошлом уроке. Заметьте ничего сложного нет. Нам удалось малыми средствами начертить равнобедренный предмет с шестью вершинами.

Его можно сделать еще проще. Например, отложить шесть радиусов на тело овала. Эта фигура не такая сложная, как с пятью или с семью углами, уроки которых мы рассмотрим в других статьях.

Я не фанат точной науки геометрии. Приходилось рисовать, но без циркуля и угольника не всегда получалось правильно создать картину.

Наша задача показать полную иллюзию пространства на двухмерной плоскости. Нарисуем многоугольник онлайн в перспективе, а для этого нужно знать правила построения.

К примеру, чтобы создать многоугольный узор на потолке, как на картине художника Премацци, нужно знать законы построения.

«Виды залов нового Эрмитажа. Галерея фламандской живописи.»

На картине Гау мы видим интерьер дворца. И все узоры выполнены в рамках законов линейной перспективы.

«Зимний дворец. Петровский зал.»

Посмотрите узор на полу в произведении Жерома Жан-Леона.

«Painting Breathes Life into Sculpture»

Задумывая сюжет в интерьере, нам придется изучать принципы построения. Как положить шестигранник на плоскость посмотрите видео урок ниже.

Симметрия

Шесть строк отражение правильного шестиугольника, с Dih₆ или r12 симметрия, порядок 12.

Диэдральные симметрии разделяются в зависимости от того, проходят ли они через вершины (d для диагонали) или краев (п для перпендикуляров) Циклические симметрии в среднем столбце помечены как г для их приказов центрального вращения. Полная симметрия правильной формы r12 и симметрия не помечена а1.

В правильный шестиугольник есть Dih₆ симметрия, порядок 12. Есть три диэдральные подгруппы: Dih₃, Ди₂, и Dih₁и четыре циклический подгруппы: Z₆, Z₃, Z₂, а Z₁.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только g6 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Пример шестиугольников по симметрии
r12регулярный i4 d6изотоксальный g6направленный p6изогональный d2 g2Общеепараллелогон p2 g3 а1

Шестиугольники симметрии g2, i4, и r12, так как параллелогоны может мозаику евклидовой плоскости переводом. Другой с разной ориентацией.

p6m (* 632)	см (2 * 22)	p2 (2222)	p31m (3 * 3)	pmg (22 *)	пг (× ×)
r12	i4	g2	d2	d2	p2	а1

Группы A2 и G2

Корни группы A2

Корни группы G2

6 корней простая группа Ли , представленный Диаграмма Дынкина , имеют правильный шестиугольный узор. Угол между двумя простыми корнями составляет 120 °.

12 корней G2, представленный Диаграмма Дынкина также имеют шестиугольную форму. Два простых корня двух длин имеют угол между собой 150 °.

Модернизированные отвертки

Профессиональный инструмент отличается дополнительным набором функций.

Конечно же, еще не была создана звуковая отвертка по образу и подобию универсальной модели из сериала «Доктор Кто», способная посредством кибернетических волн воздействовать на различные механизмы.

Но прогресс не стоит на месте, и кто знает, может в недалеком будущем человечество получит новые и суперсовременные девайсы.

Уже сейчас существуют модели, на фоне которых отвертка слесарная выглядит моделью инструмента из прошлого.

Но по-прежнему набор отверток усиленных цельнометаллических остается востребованным кейсом для специалистов самого разного профиля.

Так чем же примечательны модернизированные виды отверток?

Диэлектрические

Отвертки этого типа применяются для электромонтажных работ.

Специальная изоляция стержня отвертки защищает мастера от удара током, что позволяет использовать инструмент для откручивания деталей, находящихся под высоким напряжением.

Данный вид инструмента часто оборудуют индикатором для распознавания скрытой проводки, что позволяет «прозванивать» данные участки в целях последующего ремонта электрических сетей.

Ударные

Такой вид инструмента применяют для работы с крупными деталями, поскольку принцип его действия направлен на создание усиленного импульса.

Виды шестигранников

Если вы впервые сталкиваетесь с этим шестигранным помощником, то должны знать, что они разделяются на два вида:

• оснащенные стандартным наконечником;
• оборудованные шаром с одного края инструмента.

Второй вид шестигранных ключей дает возможность производить работы с углом наклона почти в 30 градусов, а после полного прокручивания переставлять его не требуется, в результате чего сокращается время на производство крепежных работ.

Но обойтись одним единственным шестигранным ключом одного размера вы не сможете, поэтому хорошенько обдумайте этот вопрос и приобретите полноценный разноразмерный набор внутренних шестигранников. Это самый экономный и бюджетный вариант.

Виды отверток и их назначение

Универсальная отвертка слесарная – это инструмент, который есть практически в каждом доме.

Благодаря отвертке можно выполнять ремонтные работы разной степени сложности, главное знать, какой тип и диаметр подойдет в каждом конкретном случае.

О том, какие бывают отвертки можно узнать, если детальнее углубиться в тему.

Отличительной особенностью всех видов является разное толщина стержня.

Читать также: Фрезы по металлу для фрезерного станка концевые

Наиболее популярными считают отвертки с круглым и квадратным сечением, с прямым или крестообразным шлицем.

Однако технический прогресс не стоит на месте и наряду с новыми видами крепежа появляются профессиональные отвертки для вкручивания болтов, шурупов и прочих элементов.

Все это делается для того, чтобы облегчить работу потребителям.

• На данный момент кроме универсальных моделей существует еще несколько модернизированных видов отверток для проведения разных работ.

Например, переставная отвертка отличается своей универсальностью, т.к. с одной стороны стержня она плоская, а с другой крестовая.

Некоторые переставные модели имеют несколько разных наконечников, что повышает универсальность инструмента.

• Точная или как ее еще называют, тонкая отвертка – подойдет для ремонта мобильных телефонов, ее маркировка соответствует нулевому обозначению.

Изделие производят с малым размером шлица, не более 2мм, что позволяет выполнить точную работу с мелкими деталями.

• Особые эргономичные свойства приобрела двухкомпонентная отвертка, ее отличительной особенностью стала прочная рукоять из комбинированных материалов.

Для покрытия рукояти использовали полипропилен и резину.

Двухкомпонентное покрытие способствует надежному захвату, чтобы изделие уже не могло выскользнуть из рук.

• Для работы с тонкими деталями используют часовые отвертки, с их помощью ремонтируют часовые механизмы.

Размер наконечника изделия – не более миллиметра.

На этом классификация профессиональных монтажных отверток не заканчивается, существует еще много разновидностей моделей, предназначенных для определенных целей.